Esempio calcolo integrale indefinito

 

Calcolare il seguente integrale indefinito :

 

 

Osserviamo che la quantità al denominatore della funzione integranda si può scrivere come segue

 

 

Posto quindi :

 

 

Si dovrà avere che

 

 

da cui moltiplicando e raccogliendo i fattori comuni segue che

 

 

dovrà risultare pertanto che

 

 

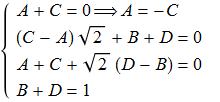
ovvero

 

 

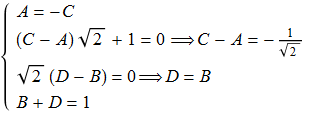
da cui

 

 

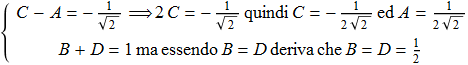
in conclusione si ottiene che

 

 

Pertanto possiamo affermare che

 

 

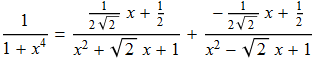
da cui

 

 

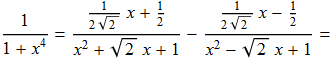
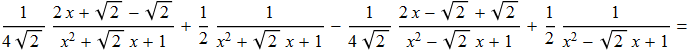
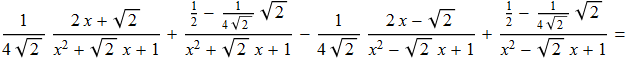
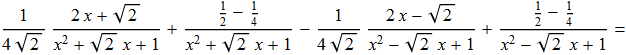
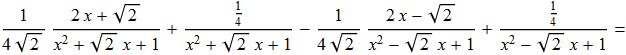
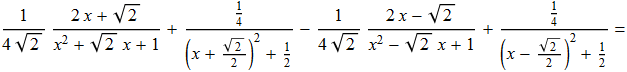
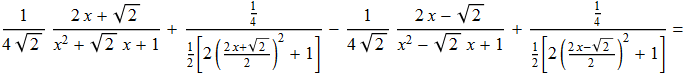
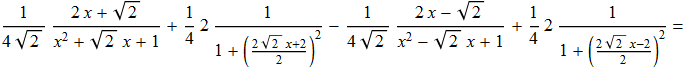
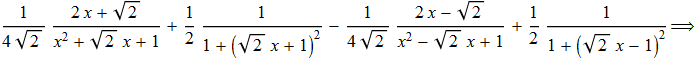
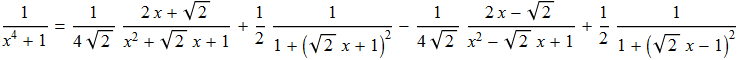
Integrando membro a membro possiamo scrivere tale relazione

 

 

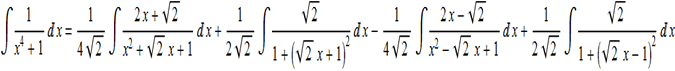
In conclusione l'integrale indefinito si potrà scrivere come segue:

 

 

 

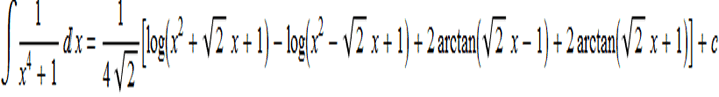
Per la versione in pdf dell'esercizio cliccare di seguito.